Proving NP-Completeness is a core topic in the studies of algorithms. For most of the algorithms textbooks, they show some complicated tricks which reduce a known NP-Complete problem to another problem, say Q, to prove that Q is NP-Complete. This works because if problem A reduces to problem B, then B is at least as difficult as A. And since A is NP-Complete, B is also NP-Complete.
However, many problem reduction methods are extremely subtle and often require some “divine instincts” to come up with in the first place. Fortunately, there is a far simpler approach to prove NP-Completeness of a problem, that is, the restriction method.
The logic of the restriction method is pretty straightforward, that is:
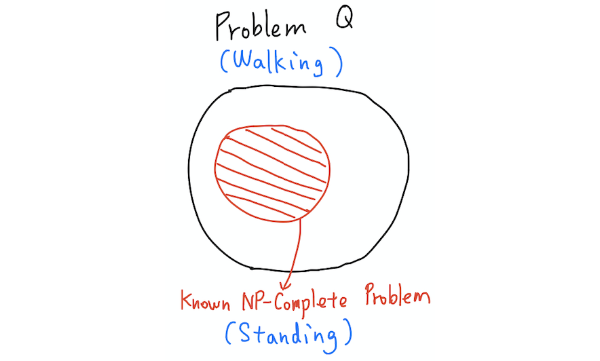
If a problem Q contains a known NP-Complete problem as its subset, then Q is also NP-Complete.
It is called the restriction method because in essence, we restrict the inputs of the problem Q to gain a subset problem of Q. And if the subset problem is NP-Complete, Q is proven to be NP-Complete.
Let’s make some analogies, suppose dribbling is hard, then you know that playing basketball is at least as difficult as dribbling, since playing basketball contains dribbling. Likewise, if standing is hard, then you know that walking is at least as difficult as standing, since standing is a subproblem of walking.
By taking this logic into the fields of algorithms, many problems could be proven to be NP-Complete within a second.
In the remaining sections of this article, I will first list some problems known to be NP-Complete, and then apply them to prove NP-Completeness of some other problems using the restriction method.
Known NP-Complete Problems
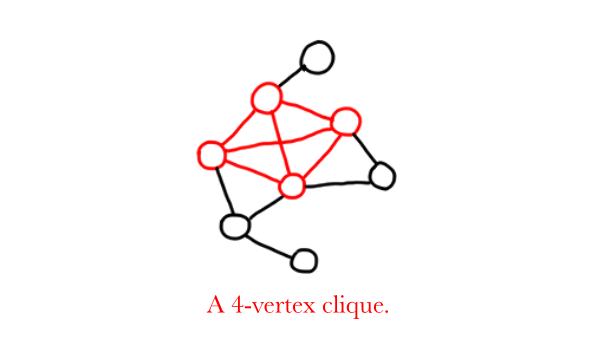
CLIQUE
Input: A graph $G=(V,E)$, and a positive integer $k$.
Problem: Return true if $G$ contains a clique of size at least $k$. Otherwise, return false. (A clique is a subset of vertices such that every two distinct vertices in the clique are adjacent. That is, the induced subgraph is complete.)
SUBSET SUM
Input: A set $S$ of integers, and an integer $W$.
Problem: Return true if there is a subset $S'$ of $S$ such that the sum of the elements of $S'$ equals to $W$. Otherwise, return false.
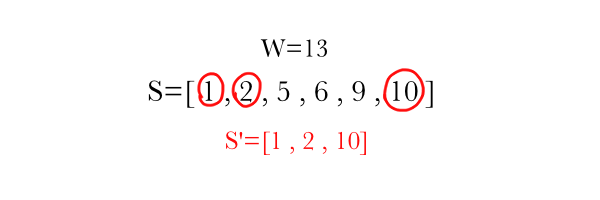
LONGEST PATH
Input: A graph $G=(V,E)$, and a number $k$.
Problem: Return true if $G$ contains a path of length at least $k$. Otherwise, return false.

HAMILTON CYCLE
Input: A graph $G=(V,E)$, and a positive integer $k$.
Problem: Return true if $G$ contains a cycle which traverses each vertex in $G$ exactly once. Otherwise, return false.
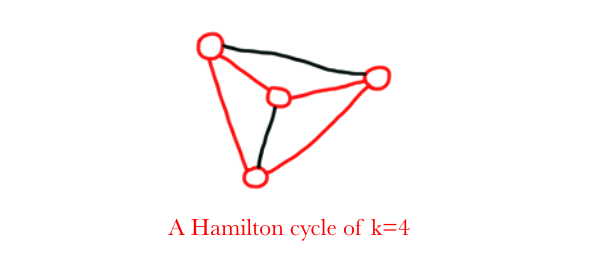
Proving NP-Completeness by Restriction
DENSEST K SUBGRAPH
Input: A graph $G=(V,E)$, a positive integer $k$, and a positive integer $l$.
Problem: Return true if $G$ contains a subgraph of $k$ vertices that has at least $l$ edges. Otherwise, return false.
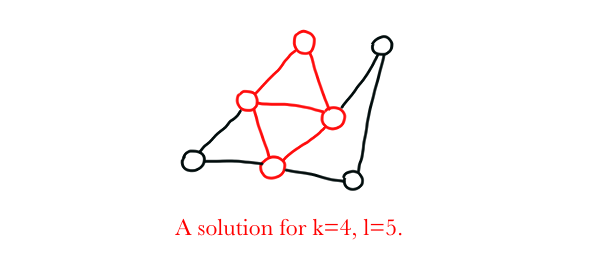
Proof: Restrict the input $l$ such that $l={k \choose 2}$. Now, we are looking for a subgraph of $k$ vertices that has at least $\frac{k(k-1)}{2}$ edges. Since $n$ vertices are allowed to have at most $\frac{n(n-1)}{2}$ edges between them, we can restate the previous goal as: “We are looking for a subgraph of $k$ vertices that has exactly $\frac{k(k-1)}{2}$ edges”. This means that the target subgraph has an edge between each pair of vertices, and thus, we are essentially searching for a clique of $k$ vertices. Since DENSEST K SUBGRAPH contains CLIQUE, it is NP-Complete.
EDGE PACKING
Input: A graph $G=(V,E)$, a positive integer $k$, and a positive integer $l$.
Problem: Return true if $G$ contains $k$ edges that are incident with at most $l$ vertices. Otherwise, return false.
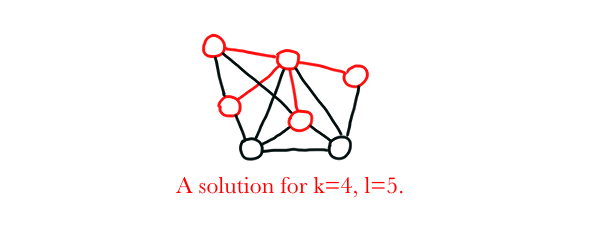
Proof: EDGE PACKING is similar to DENSEST K SUBGRAPH, but this time, we restrict $k$ such that $k={l \choose 2}=\frac{l(l-1)}{2}$. We are now looking for $\frac{l(l-1)}{2}$ edges in the graph such that they cover at most $l$ vertices. Since $\frac{l(l-1)}{2}$ edges cover exactly $l$ vertices in a graph (no more and no less), we are essentially looking for a clique with $l$ vertices. Hence, EDGE PACKING is also NP-Complete.
GRAPH CLUSTERING
Input: A graph $G=(V, E)$, a positive integer $k$, a number $d$.
Problem: Return true if $G$ contains at least $k$ vertices $V'$ such that the distance for any pair of the vertices of $V'$ is at most $d$. Otherwise, return false.
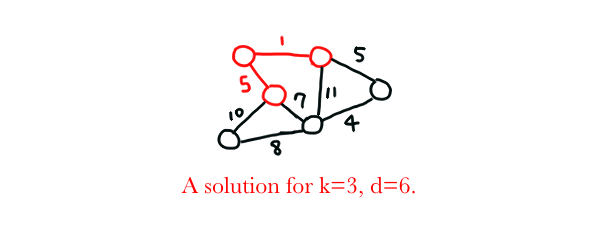
Proof: By restricting $d$ and $k$ such that $d=1$ and $k=|V|$ ($|V|$ denotes the number of vertices in graph $G$), and setting the weight of each edge such that $e_i=1$, we are now searching for a Hamilton path (that is, a longest path with length at least $k=|V|$ in a graph with each edge weighted $1$). Since HAMILTON PATH (or LONGEST PATH) is NP-Complete, GRAPH CLUSTERING is also NP-Complete.
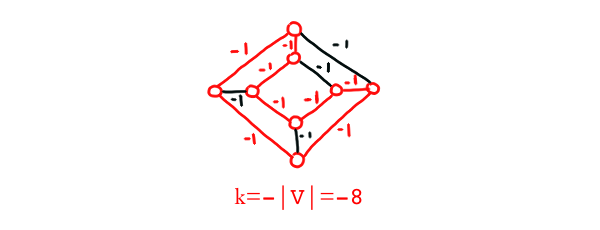
MINIMUM-WEIGHT CYCLE
Input: A graph $G=(V,E)$, a number $W$.
Problem: Return true if $G$ contains a cycle with total weight at most $W$. Otherwise, return false.
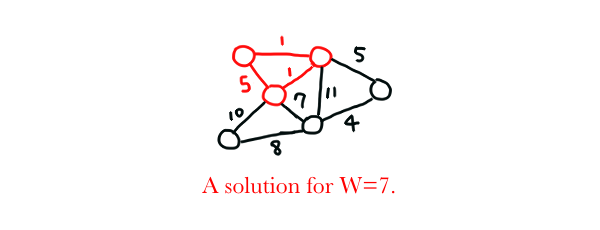
Proof: By restricting $W$ such that $W=-|V|$ and setting the weight of each edge such that $e_i=-1$, we are now looking for a Hamilton cycle with $|V|$ vertices. This is because we are required to travel $|V|$ vertices exactly once and finally get back to the initial vertex to achieve a minimum $W=-|V|$. To make the matter clearer, after traveling $|V|$ vertices, we have $W=-|V-1|$. By traveling the last edge back to the starting vertex, completing the cycle, we get $W=-|V|$ and attain our goal. MINIMUM-WEIGHT CYCLE contains HAMILTON CYCLE, so it is NP-Complete.
TILE COVER
Input: Two integers forming a dimension $w \times h$, a collection $T$ of rectangular tiles $t_i$ of integer dimension $l_i \times w_i$.
Problem: Return true if some tiles can be selected to cover exactly the whole $w \times h$ dimension. Otherwise, return false.
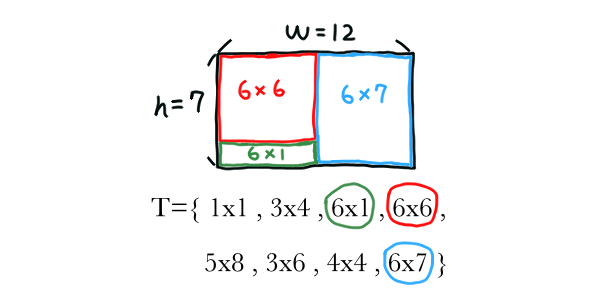
Proof: If we restrict $h$ such that $h=h_i$ for each tiles in $T$, then we only need to fit the tiles in one dimension. That is, because $h=h_i$, every tile covers the $h$-dimension fine, our problem now lies only in the $w$-dimension. It is easy to see that a one-dimensional tile cover problem is simply a subset sum problem since $T$ is only a set of integers, and our goal is a subset of $T$ with the sum of all elements equals to $w$. TILE COVER is NP-Complete because it contains SUBSET SUM.
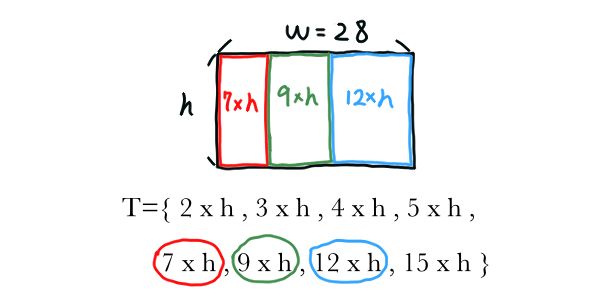
Conclusion
I want to get an A on my Design and Analysis of Algorithms course next semester. Wish me luck.